Originally posted by AtW
View Post
- Visitors can check out the Forum FAQ by clicking this link. You have to register before you can post: click the REGISTER link above to proceed. To start viewing messages, select the forum that you want to visit from the selection below. View our Forum Privacy Policy.
- Want to receive the latest contracting news and advice straight to your inbox? Sign up to the ContractorUK newsletter here. Every sign up will also be entered into a draw to WIN £100 Amazon vouchers!
Reply to: Physics question - static equilibrium
Collapse
You are not logged in or you do not have permission to access this page. This could be due to one of several reasons:
- You are not logged in. If you are already registered, fill in the form below to log in, or follow the "Sign Up" link to register a new account.
- You may not have sufficient privileges to access this page. Are you trying to edit someone else's post, access administrative features or some other privileged system?
- If you are trying to post, the administrator may have disabled your account, or it may be awaiting activation.
Logging in...
Previously on "Physics question - static equilibrium"
Collapse
-
Christ you lot are THICK.
THICK.
If you CRETINS hadn't wasted your time at school and got a proper education you would have this solved in seconds!
Leave a comment:
-
Then you'd need the sine of d and e.Originally posted by alluvial View PostAh, but try hanging two masses on the string....
Leave a comment:
-
Yay, so we're all right!Originally posted by alluvial View PostThis could be where the problem is.

Leave a comment:
-
Sorry, but suity's post wasn't complete nonsense.Originally posted by mudskipper View PostYes dear, but the opposite/adjacent thing isn't in relation to the hypotenuse, it's in relation to the angle you know - so your post was nonsense.
Here's a picture for you.
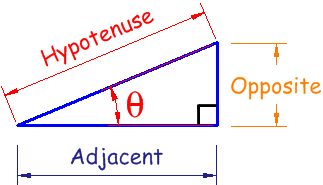
His first statement is correct and agrees with my previous post.
As the system is in static equilibrium, then the sum of the forces must equate to zero. As this is a 2D system, then you only need to consider the xy plane and so the sum of the forces acting upwards at the point of susppension must equal the downwards force created by the mass and so:
F=19 cos(a) + 12 cos(b) This is the force that stops the mass from dropping downwards.
The adjacent side in this case is the perpendicular and so cosine is used.
His second statement was (almost) wrong as this will only be true if a=b.
You then resolve the forces perpendicular to the direction in which the mass exerts a force. In this case, sine will be used and now, 19sin(a) = 12sin(b). This needs to be true to stop the mass from moving sideways.
Once you can determine what a or b are, then you can solve the first equation and then determine M by dividing by g.
Edit: BTW, I'm using a and b to be the angles obtained by subdividing the angle formed by the two suspension cables at the point of suspension.
Leave a comment:
-
Leave a comment:
-
Ooooooh, a picture, has it got kittens in it?Originally posted by mudskipper View PostYes dear, but the opposite/adjacent thing isn't in relation to the hypotenuse, it's in relation to the angle you know - so your post was nonsense.
Here's a picture for you.

No, oh, as you were then.
P.S. Suity, she called you Dear, but somehow I don't think you've pulled.
Leave a comment:
-
Yes dear, but the opposite/adjacent thing isn't in relation to the hypotenuse, it's in relation to the angle you know - so your post was nonsense.Originally posted by suityou01 View PostOooh spooky, there's an echo.
Here's a picture for you.

Leave a comment:
- Home
- News & Features
- First Timers
- IR35 / S660 / BN66
- Employee Benefit Trusts
- Agency Workers Regulations
- MSC Legislation
- Limited Companies
- Dividends
- Umbrella Company
- VAT / Flat Rate VAT
- Job News & Guides
- Money News & Guides
- Guide to Contracts
- Successful Contracting
- Contracting Overseas
- Contractor Calculators
- MVL
- Contractor Expenses
Advertisers








Leave a comment: