Reply to: Challenging Christmas Puzzle

[TimberWolf]

I started thinking about the number of solutions likely to come up, with my first guess being around the 12 digit mark, from the way previous terms had grown. But alas I got bogged down in algebra which has exhausted my time.

I started looking at the total number of arrangements of the squares (regardless of lines summing to n(n+1)/2). It's a pretty formula:

(n^2)! / (n!)^n

Which by Sterling's approximation and also hopefully after my simplification comes to :

(2pi)^0.5 . n ^ (n^2+1)
-----------------------
     (2pi.n)^(n/2)

I used to have a neat symbolic equation solver/simplifier called "Scientific Notepad", but alas that doesn't work on Vista so now all I have is my pen. Does anyone know of any decent free or very low cost maths packages that handle symbolic algebra?

Wolfram's simplification


of Sterling's expansion


of

[Spacecadet]

I went for the brute force method using SQL

First a proof of concept using a 3x3 grid where each line and diagonal = 6

with n as (
select '1' as n
union all
select '2' as n
union all
select '3' as n
) ,
r as (
select n1.n c1, n2.n c2, n3.n c3
from n n1
cross join n n2
cross join n n3
where cast(n1.n as int) + cast(n2.n as int) + cast(n3.n as int) = 6
)
select r1.c1 as r1c1,r1.c2 as r1c2, r1.c3 as r1c3,
       r2.c1 as r2c1,r2.c2 as r2c2, r2.c3 as r2c3,
       r3.c1 as r3c1,r3.c2 as r3c2, r3.c3 as r3c3
from r r1
cross join r r2
cross join r r3
where 
    len(replace(
    r1.c1+r1.c2+r1.c3+
    r2.c1+r2.c2+r2.c3+
    r3.c1+r3.c2+r3.c3, '1', '')) = 6
and 
    len(replace(
    r1.c1+r1.c2+r1.c3+
    r2.c1+r2.c2+r2.c3+
    r3.c1+r3.c2+r3.c3, '2', '')) = 6
and 
    len(replace(
    r1.c1+r1.c2+r1.c3+
    r2.c1+r2.c2+r2.c3+
    r3.c1+r3.c2+r3.c3, '3', '')) = 6
and 
    cast(r1.c1 as int) + CAST(r2.c2 as int) + CAST(r3.c3 as int) = 6
and 
    cast(r1.c3 as int) + CAST(r2.c2 as int) + CAST(r3.c1 as int) = 6
and 
    cast(r1.c1 as int) + CAST(r2.c1 as int) + CAST(r3.c1 as int) = 6    
and 
    cast(r1.c2 as int) + CAST(r2.c2 as int) + CAST(r3.c2 as int) = 6        
and 
    cast(r1.c3 as int) + CAST(r2.c3 as int) + CAST(r3.c3 as int) = 6

Expanding this to a 5x5 grid:

with n as (
select '1' as n
union all
select '2' as n
union all
select '3' as n
union all
select '4' as n
union all
select '5' as n
) ,
r as (
select n1.n c1, n2.n c2, n3.n c3, n4.n c4, n5.n c5
from n n1
cross join n n2
cross join n n3
cross join n n4
cross join n n5
where cast(n1.n as int) + cast(n2.n as int) + cast(n3.n as int) + cast(n4.n as int) + cast(n5.n as int) = 15
)
select r1.c1 as r1c1,r1.c2 as r1c2, r1.c3 as r1c3, r1.c4 as r1c4, r1.c5 as r1c5,
       r2.c1 as r2c1,r2.c2 as r2c2, r2.c3 as r2c3, r2.c4 as r2c4, r2.c5 as r2c5,
       r3.c1 as r3c1,r3.c2 as r3c2, r3.c3 as r3c3, r3.c4 as r3c4, r3.c5 as r3c5,
       r4.c1 as r4c1,r4.c2 as r4c2, r4.c3 as r4c3, r4.c4 as r4c4, r4.c5 as r1c5,
       r5.c1 as r5c1,r5.c2 as r5c2, r5.c3 as r5c3, r5.c4 as r5c4, r5.c5 as r1c5
from r r1
cross join r r2
cross join r r3
cross join r r4
cross join r r5
where 
    len(replace(
    r1.c1+r1.c2+r1.c3+r1.c4+r1.c5+
    r2.c1+r2.c2+r2.c3+r2.c4+r2.c5+
    r3.c1+r3.c2+r3.c3+r3.c4+r3.c5+
    r4.c1+r4.c2+r4.c3+r4.c4+r4.c5+
    r5.c1+r5.c2+r5.c3+r5.c4+r5.c5, '1', '')) = 20
and 
    len(replace(
    r1.c1+r1.c2+r1.c3+r1.c4+r1.c5+
    r2.c1+r2.c2+r2.c3+r2.c4+r2.c5+
    r3.c1+r3.c2+r3.c3+r3.c4+r3.c5+
    r4.c1+r4.c2+r4.c3+r4.c4+r4.c5+
    r5.c1+r5.c2+r5.c3+r5.c4+r5.c5, '2', '')) = 20
and 
    len(replace(
    r1.c1+r1.c2+r1.c3+r1.c4+r1.c5+
    r2.c1+r2.c2+r2.c3+r2.c4+r2.c5+
    r3.c1+r3.c2+r3.c3+r3.c4+r3.c5+
    r4.c1+r4.c2+r4.c3+r4.c4+r4.c5+
    r5.c1+r5.c2+r5.c3+r5.c4+r5.c5, '3', '')) = 20
and 
    len(replace(
    r1.c1+r1.c2+r1.c3+r1.c4+r1.c5+
    r2.c1+r2.c2+r2.c3+r2.c4+r2.c5+
    r3.c1+r3.c2+r3.c3+r3.c4+r3.c5+
    r4.c1+r4.c2+r4.c3+r4.c4+r4.c5+
    r5.c1+r5.c2+r5.c3+r5.c4+r5.c5, '4', '')) = 20
and 
    len(replace(
    r1.c1+r1.c2+r1.c3+r1.c4+r1.c5+
    r2.c1+r2.c2+r2.c3+r2.c4+r2.c5+
    r3.c1+r3.c2+r3.c3+r3.c4+r3.c5+
    r4.c1+r4.c2+r4.c3+r4.c4+r4.c5+
    r5.c1+r5.c2+r5.c3+r5.c4+r5.c5, '5', '')) = 20
and 
    cast(r1.c1 as int) + CAST(r2.c2 as int) + CAST(r3.c3 as int) + CAST(r4.c4 as int) + CAST(r5.c5 as int) = 15
and 
    cast(r1.c5 as int) + CAST(r2.c4 as int) + CAST(r3.c3 as int) + CAST(r4.c2 as int) + CAST(r5.c1 as int) = 15    
and 
    cast(r1.c1 as int) + CAST(r2.c1 as int) + CAST(r3.c1 as int) + CAST(r4.c1 as int) + CAST(r5.c1 as int) = 15    
and 
    cast(r1.c2 as int) + CAST(r2.c2 as int) + CAST(r3.c2 as int) + CAST(r4.c2 as int) + CAST(r5.c2 as int) = 15        
and 
    cast(r1.c3 as int) + CAST(r2.c3 as int) + CAST(r3.c3 as int) + CAST(r4.c3 as int) + CAST(r5.c3 as int) = 15        
and 
    cast(r1.c4 as int) + CAST(r2.c4 as int) + CAST(r3.c4 as int) + CAST(r4.c4 as int) + CAST(r5.c4 as int) = 15        
and 
    cast(r1.c5 as int) + CAST(r2.c5 as int) + CAST(r3.c5 as int) + CAST(r4.c5 as int) + CAST(r5.c5 as int) = 15

This found almost 60,000 solutions in 22 minutes - at which point I stopped it!

[TimberWolf]

Incidentally the number of solutions, as a proportion of all possible unique combinations (not necessarily summing to n(n+1)2, is reducing exponentially, even if the number of those unique combinations is increasing at an exponentially greater rate.
i.e.

n      solutions      unique combinations      col3  / col 2 

1          1                     1                1 in 1
2          0                     6                undefined
3          4                  1680                1 in 420
4        256              6 * 10^7                1 in 3/4 million
5    836,864             6 * 10^14                1 in 740 million

[TimberWolf]

using Monte Carlo simulation and methods from statistical mechanics.

I briefly considered using statistical methods to approximate what the answer would be, by counting the number of invalid combinations tried before a valid one was found. But given that there are 2.7*10^24 arrangements, the likelihood of finding a solution by chance in a reasonable amount of time seemed too small. A program that swaps two squares if the resulting arrangement is closer to a valid solution does quickly find solutions though, and it's possible some kind of analysis could be done on that.

[OwlHoot]

I started thinking about the number of solutions likely to come up, with my first guess being around the 12 digit mark, from the way previous terms had grown. But alas I got bogged down in algebra which has exhausted my time.

I started looking at the total number of arrangements of the squares (regardless of lines summing to n(n+1)/2). It's a pretty formula:

(n^2)! / (n!)^n

Which by Sterling's approximation and also hopefully after my simplification comes to :

(2pi)^0.5 . n ^ (n^2+1)
-----------------------
     (2pi.n)^(n/2)

I used to have a neat symbolic equation solver/simplifier called "Scientific Notepad", but alas that doesn't work on Vista so now all I have is my pen. Does anyone know of any decent free or very low cost maths packages that handle symbolic algebra?

Just replace each factorial by Stirling's Approximation

This is a divergent series whose truncations give very accurate approximations, e.g.

n! = SQRT(2 PI n) (n / e)^n (1  +  1 / (12 n))

I don't think it's as simple as that though, because all the sums, and the requirement to use a given set of numbers impose extra, and arguably "artificial", conditions.

Incidently, the number of magic squares (a closely related construct) of order 6 is currently unknown, but believed to be about 1.7 * 10^19, and this enumeration is probably tougher than even that!

It is an unsolved problem to determine the number of magic squares of an arbitrary order, but the number of distinct magic squares (excluding those obtained by rotation and reflection) of order n=1, 2, ... are 1, 0, 1, 880, 275305224, ... (Sloane's A006052; Madachy 1979, p. 87). The 880 squares of order four were enumerated by Frénicle de Bessy in 1693, and are illustrated in Berlekamp et al. (1982, pp. 778-783). The number of 5×5 magic squares was computed by R. Schroeppel in 1973. The number of 6×6 squares is not known, but Pinn and Wieczerkowski (1998) estimated it to be (1.7745+/-0.0016)×10^(19) using Monte Carlo simulation and methods from statistical mechanics.

edit: Oops, sorry, missed the bit where you said you already used Stirling's approximation. I'll think about it some more when I'm sober :-)

[TimberWolf]

I started thinking about the number of solutions likely to come up, with my first guess being around the 12 digit mark, from the way previous terms had grown. But alas I got bogged down in algebra which has exhausted my time.

I started looking at the total number of arrangements of the squares (regardless of lines summing to n(n+1)/2). It's a pretty formula:

(n^2)! / (n!)^n

Which by Sterling's approximation and also hopefully after my simplification comes to :

(2pi)^0.5 . n ^ (n^2+1)
-----------------------
     (2pi.n)^(n/2)

I used to have a neat symbolic equation solver/simplifier called "Scientific Notepad", but alas that doesn't work on Vista so now all I have is my pen. Does anyone know of any decent free or very low cost maths packages that handle symbolic algebra?

[OwlHoot]

The trouble is the count for n=6 may be so large that just incrementing a count from zero to the required size (and doing nothing else) might take months or years, and clearly that is an (unattainable) lower bound on any "try all cases" procedure.

But if not then my "fold and unfold" approach might come into its own for n=6, although some of the details would need generalizing and simplifying (even at the cost of making it sub-optimal).

edit: For n=6 (or any even n) the row and column "flip and adds" AKA merges don't leave an "unaffected apart from doubling" central row and column respectively, and that improves the array element equalization in these stages :

Original n=6 array:

 a11  a12  a13  a14  a15  a16

 a21  a22  a23  a24  a25  a26

 a31  a32  a33  a34  a35  a36

 a41  a42  a43  a44  a45  a46

 a51  a52  a53  a54  a55  a56

 a61  a62  a63  a64  a65  a66

After row flip-and-add :

 b11  b12  b13  b14  b15  b16

 b21  b22  b23  b24  b25  b26

 b31  b32  b33  b34  b35  b36

 b31  b32  b33  b34  b35  b36

 b21  b22  b23  b24  b25  b26

 b11  b12  b13  b14  b15  b16

After column flip-and-add:

 c11  c12  c13  c13  c12  c11

 c21  c22  c23  c23  c22  c21

 c31  c32  c33  c33  c32  c31 

 c31  c32  c33  c33  c32  c31 

 c21  c22  c23  c23  c22  c21

 c11  c12  c13  c13  c12  c11

After right diagonal flip-and-add :

 2 c11   d12    d13    d13    d12    d11

  d12   2 c22   d23    d23    d22    d12

  d13    d23   2 c33   d33    d23    d13 

  d13    d23    d33   2 c33   d23    d13 

  d12    d22    d23    d23   2 c22   d12

  d11    d12    d13    d13    d12   2 c11

So that leaves only the 6 distinct elements: c11, c22, c33, d12, d13, d23, in an array whose rows, columns, and main diagonals must sum to 8 * 21,
and it shouldn't take long to find all combinations of the latter with 4 <= c_ij <= 24 and 8 <= d_ij <= 48.

[Platypus]

Update for anyone WGAS

I'm trying to make my code run absolutely as fast as possible, while generalising it for grids larger than 5x5.

I've pruned several minutes, but the largest improvement has come from running it natively under MSVC (v6) rather than under the old 'MKS NuTCracker' environment (which is what I was using).

At this point, I can solve the 5x5 problem in approx 4:20 minutes (from a possible 21 billion combinations). However, a 6x6 grid offers 4332^5 combinations (assuming the last row is calculated). Which is 72 million times more.

So maybe I can solve 6x6 in 72 million x 5 minutes = 688 years

On the other hand, one can slide and dice this calculation various ways, so I'm going to write the code for a 6x6 and see what happens.

I'll post the result, hopefully in less than 688 years.

I am just going outside and may be some time ...

[TimberWolf]

But if you enumerate the 6*6 solutions, why not submit the sequence 1, 0, 256, 836864, ? to the Sloane On-Line Encyclopedia of Integer Sequences™ (OEIS™) and get your name(s) in lights ?

The honour is Platypus'.

As for the next count in that sequence, I've noticed that it's divisible by the last. 836,864 is divisible by 256, etc. At first I had 'aha, of course' moment, as one grid is inside another and can be combined inside the new extra squares making up a bigger grid, and combined again each time the new surrounding squares are rearranged. But after a bit more thought it became less obvious that that should be the case.

[OwlHoot]

No way can I afford to spend any more time on this problem. (Get thee behind me Satan!) So for that reason I'm out.

But if you enumerate the 6*6 solutions, why not submit the sequence 1, 0, 256, 836864, ? to the Sloane On-Line Encyclopedia of Integer Sequences™ (OEIS™) and get your name(s) in lights ?

The first count should definitely be 1, as a single element equal to 1 trivially satisfies all the conditions, and there's currently no OEIS sequence 1, 0, 4, 256

BTW I didn't get any very useful replies from my post elsewhere, except to confirm your 5*5 result

[Platypus]

I suspect that your own contributions to a proposed solution offer the best hope. The final version of that did a mere 75 million checks compared with 3 odd billion for the "381^4" version.

I may have a noodle, but maybe later !

[TimberWolf]

Who fancies a go at this then?



Are you hard enough? It should keep brute force methods busy for a while. Rows sum to 21 in this 6*6 case.

Here's one solution:

2 3 1 6 3 6
6 4 4 2 4 1
3 2 4 1 6 5
5 5 5 4 1 1
3 3 1 3 5 6
2 4 6 5 2 2

I'm not going to try to brute force that grid to find all solutions, I'd prefer to see whether Owlhoot can crack his method (whatever it is) with the 5*5 grid first. Though even if that did work, the question would be whether 6*6 and above would be tractable, or whether it's just a slightly quicker brute force method.


Here's a summary of how (I believe) things stand for grid sizes up to 7:

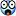
Table   Rows sum     Platypus     Solutions
size       to         number

1*1        1            1            0 (or 1)
2*2        3            2            0
3*3        6            7            4
4*4       10           44          256
5*5       15          381      836,864
6*6       21        4,332            ?
7*7       28       60,691            ?

I did a quick run on table sizes 1*1 to 4*4 to find their numbers of solutions above. You can see how the number of solutions is climbing at an exponential rate, which if continued unbridled might be a killer even for optimised algorithms, as if there are trillions of trillions of solutions, they are going to take time to produce no matter how elegant the algorithm, unless that value can be found without going through them all and counting them one at a time.

[TimberWolf]

Yup, that sounds like the right answer - Congratulations. I've made enquiries on a couple of puzzle forums, so it'll be interesting to see if there are any replies from that, and I'll post any info that turns up.

I've checked my code and can't see anything obviously wrong, like using x23 instead of x12 or something after a copy and paste, although God knows there are double indexes all over the place as you can imagine and I may have missed one.

I think what may be happening is that one of my loop bounds is 2 - 10 instead of 4 - 20 or something like that (given how my approach is supposed to work).

I guess there's a moral there about software development in general - It isn't worth trying too hard to develop a complicated optimized algorithm for a one-off problem when a simpler approach gets the answer in a reasonable time (although when you mentioned a running time of 12 years, I thought that was necessary for this problem!)

Since we have more solutions than yourself (5 times as many), perhaps it would help if I pasted a few here. I can present them in a numerically sorted order, so if you are to also sort them, there's a chance the missing ones can be spotted. I'll post the first 10 solutions (and I've plenty more where they came from):

11355 14424 55212 42351 43323
11355 14433 55221 52242 33414
11355 14514 45321 52242 43233
11355 14514 54222 43251 43323
11355 14523 44223 52251 44313
11355 14523 44322 51342 45123
11355 14523 45231 52242 43314
11355 14523 45321 51243 44223
11355 14523 54213 42351 44223
11355 14532 54213 52341 34224


Or in an easier to read format, the same 10:

11355
14424
55212
42351
43323

11355
14433
55221
52242
33414

11355
14514
45321
52242
43233

11355
14514
54222
43251
43323

11355
14523
44223
52251
44313

11355
14523
44322
51342
45123

11355
14523
45231
52242
43314

11355
14523
45321
51243
44223

11355
14523
54213
42351
44223

11355
14532
54213
52341
34224

[TimberWolf]

EDIT: small modification to program gives 960 solutions where each row, column and both diagonals contain 1,2,3,4,5

I can confirm 960.

[OwlHoot]

Excellent work! I guess that’s the puzzle solved. ..

Yup, that sounds like the right answer - Congratulations. I've made enquiries on a couple of puzzle forums, so it'll be interesting to see if there are any replies from that, and I'll post any info that turns up.

I've checked my code and can't see anything obviously wrong, like using x23 instead of x12 or something after a copy and paste, although God knows there are double indexes all over the place as you can imagine and I may have missed one.

I think what may be happening is that one of my loop bounds is 2 - 10 instead of 4 - 20 or something like that (given how my approach is supposed to work).

I guess there's a moral there about software development in general - It isn't worth trying too hard to develop a complicated optimized algorithm for a one-off problem when a simpler approach gets the answer in a reasonable time (although when you mentioned a running time of 12 years, I thought that was necessary for this problem!)